Problem Solving

July 5, 2019 By B. Baylis Leave a Comment

Archimedes: A Great Mathematician, But Very Eccentric

An 1810 pencil and paper sketch of Archimedes by an unknown artist. The original is located in the Museum of Fine Arts in Rio de Janeiro. As a photographic image of a two-dimensional work of art in the public domain, it is also in the public domain. Image courtesy of Wikimedia Commons and the Museum of Fine Arts, Rio de Janeiro.

Some might claim that the two phrases that I used to describe Archimedes in the title of this post say the same thing. Even though mathematicians have the reputation of being strange, I am honored, but humbled to claim the mantle of a mathematician. The roles and duties of a mathematician are to identify and solve problems, to quantify and count those things that can be enumerated, to unfold and qualify those things which can’t be enumerated, and to discover and disseminate the beauty of patterns within this world.

I know my work as a mathematician is overshadowed by many great mathematicians like Archimedes. It is still my calling. Image courtesy of Presenter Media.

It is a big job. However, I was called to this vocation and I love it. I know that my mathematical accomplishments will hold a candle to those of Archimedes. Nevertheless, I count it a privilege to work in the shadow of Archimedes, Pythagoras, and so many others.

According to the many legends about Archimedes, the opening sketch shows him in what would have been a typical pose for him: deep in thought pondering a mathematical, geometric, or engineering problem, tinkering with some toy, piece of equipment, or prototype. Archimedes was the archetypical professor, preoccupied in his thoughts to the exclusion of everything else.

Map of Sicily c 431 B.C., showing the city of Syracuse of its Eastern coast. Abu America, copyright holder has licensed its use under the Creative Commons Attribution-Share Alike 3.0 Unported license. Image courtesy of Abu America and Wikimedia Commons.

It is believed that Archimedes was born sometime in the year 287 BC, in the city of Syracuse on the island of Sicily. His father, Phidias, was a well-known astronomer and mathematician, and a relative of the King of Syracuse. As a young child, Archimedes was tutored by the best teachers in Italy. In his teen years, he reportedly traveled to Egypt and studied under their greatest teachers, mathematicians, scientists, and engineers. In his early twenties, he returned to Syracuse where he lived the remainder of his life, solving problems and corresponding with his Egyptian colleagues.

Engraving of Archimedes moving the world with his lever from Mechanic’s Magazine (cover of bound Volume II, Knight & Lacey, London, 1824). It is in the public domain because it was published prior to 1924. Courtesy of Wikimedia Commons and the Annenberg Rare Book & Manuscript Library, University of Pennsylvania, Philadelphia

I first became acquainted with Archimedes as a fourth-grader, when our teacher introduced the topic of levers during a science lesson on simple tools. The teacher began his demonstration by using an exaggerated statement he attributed to Archimedes: “Give me a place to stand and a lever long enough, I can move the world.”

In the mid-1950s, at least five years prior to human space travel, we all knew that this was a physical impossibility. But it actually made some sense, as we constructed our own levers to move objects.

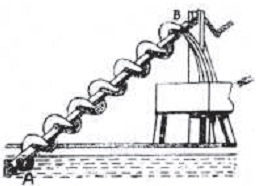
Archimedes’ screw has been used for centuries as a means of transferring water from a low-lying body to a higher level. This example is a sketch of a working screw from the University of Mysore, Karnataka, India, which has licensed the image under the Creative Commons Attribution-Share Alike 3.0 Unported License. Image courtesy of Wikimedia Commons and University of Mysore

By the time our teacher introduced the Archimedes screw in a subsequent lesson as an example of another simple tool, I was hooked. I was an Archimedes fan.

This guy rocked. One year earlier, I had “helped” my father build an automatic stoker for the coal furnace in our house using an auger that he bought from a farmer that no longer needed it to carry feed to the milking herd that he had sold. That auger was an exact replica of Archimedes’ screw. My father used it to move coal horizontally rather than moving water vertically.

Diagram of Archimedes Method for Solving Problems. Chart created by blog’s author using Click Charts software.

As our teacher told us more about Archimedes, I found that he would take both seemingly simple and complex, real-world problems and use the principles of engineering, physics, and mathematics to solve them. As our teacher systematically detailed the six steps in Archimedes’ method for solving problems, they were indelibly fixed in my mind.

Although I may have demonstrated some of the engineering brilliance of Archimedes, I haven’t yet talked about any of his mathematical work or any of his eccentricities. What were some of the mathematical problems that Archimedes attacked and solved?

It was well known by the time of Archimedes that there was a constant relationship between the radius of a circle and both its circumference and area. We now know this constant as pi or π. Although the use of the Greek letter π was not adopted for general use until the 18th century AD, for the sake of brevity and clarity I will use it for the remainder of this blog. Since Archimedes was generally considered the first to document an attempt to approximate this constant as closely as possible, it is sometimes called Archimedes’ constant.

By 1900 BC, Babylonians had estimated that π was approximately 25/8. In the same time period, Egyptians began using a value of 256/81. The decimal representation of fractions can be traced back to China by the 4th century BC, before slowly spreading through Asia, to the Middle East, and then to Europe. Europeans didn’t fully adopt this approach to expressing non-integral values until they had embraced the base-ten, positional Hindu-Arabic number system that we use today. Thus, we can say that the Babylonians estimated that π was approximately 3.125, while the Egyptians estimated that π was approximately 3.1605.

This image of Solomon’s Temple shows the great basin in the left foreground. As a faithful reproduction of a two-dimensional work of art in the public domain, it is in the public domain. Image courtesy of Wikimedia Commons.

A millennium later we find the ancient Israelites using “3” as an estimate of π in a Biblical reference related to the design of Solomon’s temple.

And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about. (I Kings 7:23, KJV)

The molten sea was actually a large bronze basin filled with water meant to symbolize the chaos of the world during creation when God’s spirit moved upon the waters.

And the earth was without form, and void; and darkness was upon the face of the deep. And the Spirit of God moved upon the face of the waters. (Genesis 1:2, KJV)

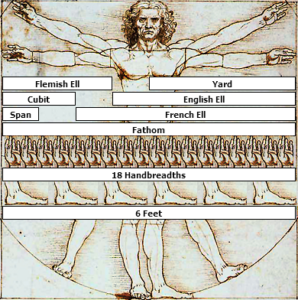
his derivation of the Vitruvian Man by Leonardo Da Vinci depicts nine historical units of measurement: the Yard, the Span, the Cubit, the Flemish Ell, the English Ell, the French Ell, the Fathom, the Hand , and the Foot. Da Vinci drew the Vitruvian man to scale, so the units depicted here are displayed with their proper historical ratios. The creator of the work and the copyright holder, Unitfreak, has released the work into the public domain. Image courtesy of Unitfreak and Wikimedia Commons.

Simple mathematics would tell us that if the diameter of the basin was 10 cubits and its circumference was 30 cubits, the ratio of circumference to diameter was “3.” This is “short” of our current value of π. However, there is a “fudge” factor built into the biblical account. A cubit was never a precise measurement. A cubit was generally considered the length of the forearm of a typical man which is the distance from the elbow to the tip of a man’s middle finger. It was generally about 18 inches or 44 centimeters. However, it could vary with each person making the measurement.

This imprecision didn’t sit well with mathematicians or builders. Although a few mathematicians worked on this problem, it took almost another millennium for Archimedes to come up with a different approach to the problem.

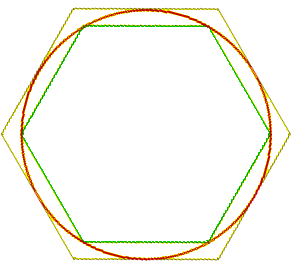
The starting point of Archimedes’ calculation of π is a circle of diameter 1, with inscribed and circumscribed hexagons. This image was uploaded to Hebrew Wikipedia by דוד שי who licensed its use under the Creative Commons Attribution-Share Alike 3.0 Unported license. Image courtesy of דוד שי and Wikimedia Commons.

Archimedes tackled the problem of calculating the circumference of a circle using an iterative approach and an over-and-under perspective. He inscribed and circumscribed hexagons inside and outside a circle with a diameter of 1. He was able to calculate the circumferences of the two hexagons, using only the following two results:

1. Pythagorean Theorem: The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.

( a² + b² = c² )

2. Proposition 3 of Book IV of Euclid’s Elements: If an angle of a triangle be bisected and the straight line cutting the angle cut the base also, the segments of the base will have the same ratio as the remaining sides of the triangle; and, if the segments of the base have the same ratio as the remaining sides of the triangle, the straight line joined from the vertex to the point of section will bisect the angle of the triangle.

Using these two results Archimedes converted the geometric problem to strictly an algebraic problem, howbeit a complicated one. He then iterated the process by successively doubling the number of polygons which inscribed and circumscribed the circle with a diameter of 1. By the time he was using 96 polygons, he had narrowed down the upper and lower limits of π to 3.1408 and 3.1428. This approximation is accurate to two decimal places, which is accurate within 0.4%.

Archimedes’ sphere and circumscribing cylinder. This image was created by André Karwath. It is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license. Image courtesy of André Karwath and Wikimedia Commons.

The mathematical problem that Archimedes claimed to be proudest of solving was finding the volume and surface area of a sphere. Archimedes showed that the volume of the sphere has 2/3 the volume and surface of the circumscribing cylinder. Thus, the surface area and volume of a sphere with radius r are given by the equations:

A = 4 πr²

and

V = (4/3)πr³.

Cicero discovering the tomb of Archimedes in an 1897 painting by Benjamin West. As a faithful reproduction of a two-dimensional work of art in the public domain, it is in the public domain. Image courtesy of Bridgeman Art Library and Wikimedia Commons.

Archimedes was so proud of this mathematical accomplishment that he requested that a cylinder encasing a sphere adorn his tomb when he died. This is how the tomb of Archimedes was eventually identified.

In 75 BC, 137 years after Archimedes’ death, the Roman statesman and philosopher Cicero in his Tusculan Disputations Book V, Sections 64 – 66, wrote the following:

When I was questor in Sicily I managed to track down his grave. The Syracusians knew nothing about it, and indeed denied that any such thing existed. But there it was, completely surrounded and hidden by bushes of brambles and thorns. I remembered having heard of some simple lines of verse which had been inscribed on his tomb, referring to a sphere and cylinder modelled in stone on top of the grave. And so I took a good look round all the numerous tombs that stand beside the Agrigentine Gate. Finally I noted a little column just visible above the scrub: it was surmounted by a sphere and a cylinder.

Probably the most famous incident that illustrated Archimedes’ single-mindedness and his eccentricities involved a royal crown and a bath. Archimedes was the go-to-guy in ancient Syracuse to solve problems. Thus, when the Hiero II, King of Syracuse was faced with the suspicion that he had been cheated by a dishonest artisan, he asked for Archimedes’ help.

Heiro II commissioned the creation of a solid gold crown to adorn statues of the gods and goddesses of Syracuse. Since the crown was to be part of a worship activity, Heiro didn’t want to offend the divines. He had to be sure that it was really solid gold, but he couldn’t melt down the crown to find its makeup. So he asked Archimedes to determine a way to test the crown without disturbing or disfiguring it.

Woodcut print from the book “Historical and critical information about the life, inventions and writings of Archimedes of Syracuse” by Count Giammaria Mazzuchelli (1707-1765), published in Brescia, Italy in 1737. As a faithful reproduction of a public domain work, it is in the public domain. Image courtesy of Wikimedia Commons.

In the most famous legend associated with this storying Archimedes was thinking about how to solve this problem while he was taking a bath in one of the public baths of the day. According to the legend, as Archimedes began to submerge himself, he realized that his body mass was displacing an equal mass of water. Here was the solution. Archimedes suddenly screamed “Eureka!” and jumped up and ran home to test his solution. In his haste, he forgot his clothes, so supposedly he was running through the streets of Syracuse naked, yelling “Eureka!” which means “I found it!“

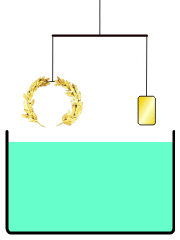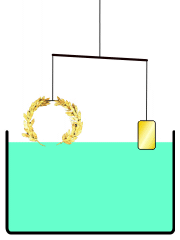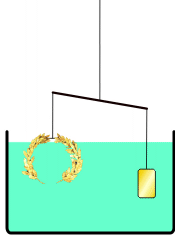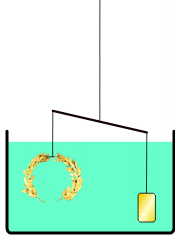
As gold mass equal in weight to the crown are submerged, if the crown rises toward the surface, it has less gold in it.

Although there are many versions of this story, I tend to believe the following one is the most plausible. This version is attributed to Vitruvius, a Roman architect of the first century BC. The Archimedes buoyancy principle may have been used to determine whether the golden crown was less dense than gold. Given that both the crown (left) and the reference weight (right) are of identical volume, the less dense reference weight object will experience a larger upward buoyant force, causing it to weigh less in the water and float closer to the surface.

This depiction of the Claw of Archimedes from a 17th-century wall painting by Giulio Parigi expresses visually uses the literal translation of the Italian word for claw as a giant iron hand. As the faithful reproduction of a two-dimension work of art in the public domain, it is in the public domain. The original is in Room 17 of The Stanzino delle Matematiche of the Uffizi Gallery in Florence. Image courtesy of Uffizi Gallery and Wikimedia Commons.

When Syracuse was attacked by Roman naval forces, King Heiro II also commissioned Archimedes to invent weapons to defend the city. According to the legends, Archimedes responded with two monstrous creations. The first was known as the Claw of Archimedes.

It was a giant crane with a long line with a hook that caught the bow of any ship that ventured too close to the seawalls defending Syracuse. By raising and lowering the crane arm, it was able to swamp and/or overturn the boat caught by the hook. It only took one or two encounters with this weapon for the Romans to learn to stay far enough away from the seawall.

Conceptual drawing of Archimedes Death Ray using polished mirrors to concentrate enough sunrays to set Roman ships afire. The drawing is by Finnrind and is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Image courtesy of Finnrind and Wikimedia Commons.

With the Roman boats now staying a bowshot away from the shore, Archimedes was challenged to come up with another weapon to defeat this persistent enemy. This led to the legend of Archimedes’ Death Ray. Most every small child knows that using a magnifying glass or a parabolic mirror, one can start a fire from the sun’s rays. According to the stories, Archimedes used this principle to set the Roman ships afire.

Over the intervening centuries, many experiments have been done to try to recreate the incendiary events. In all cases, more mirrors than shown would be needed, and the usual results may have been temporary blindness and confusion among the sailors rather than fire.

Since there are Roman accounts of ships burning and sinking, something probably happened. The mirrors may have consisted of polished metal and had peep-holes drilled in the middle for use in aiming. Whether they set the Roman ship afire, or just created enough confusion so that small crafts from the defenders of Syracuse could get close enough to fling burning vats of “Greece fire,” i.e., burning oil, will never be known.

The Roman commander Marcellus knew through the tales of spies and traitors that the machines that Archimedes had invented caused the problems for his troops. He laid siege to the city and after a protracted period of time, finally wore them down due to the lack of supplies. He ordered his troops to destroy everything and everyone with one exception. Under no circumstances was Archimedes to be harmed. He was to be taken alive. Marcellus wanted this genius working for him.

A print from the biography of Archimedes written by Giammaria Mazzucchelli from 1737. This is a faithful reproduction of a two-dimensional public domain work of art contained in the Vatican Library. Thus, it is in the public domain. Image courtesy of the Vatican Library and Wikimedia Commons.

Here is where the single-mindedness of Archimedes got the eccentric in trouble again. A soldier found Archimedes working on a mathematics problem drawing circles in the sand. The soldier ordered Archimedes to come with him. Archimedes told the soldier he couldn’t because he was in the middle of solving an important problem. The soldier started scratching out the sand circles. Archimedes yelled at the soldier “Nōlī turbāre circulōs meōs!” a Latin phrase, meaning “Do not disturb my circles!”

The soldier got angrier with Archimedes and killed him. When this was reported to Marcellus, he ordered the soldier killed, and Archimedes to be given a burial befitting royalty. Hence the fancy tomb that we had noted that was discovered by Cicero. Archimedes was indeed an eccentric, as well as a mathematical and engineering genius.

In my next post, I will return to considering some of the crisis facing modern American higher education. The next crisis on the agenda is the crisis centered on and created by the Faculty Reward Systems and Faculty Priorities. I hope to post it next week.

April 16, 2019 By B. Baylis 1 Comment

Are All Mathematicians Crazy?

Crazy mathematician playing with his computer. Image courtesy of Presenter Media.

I personally guarantee it. “Not all mathematicians are crazy.” You can take it from me that some of us are almost normal. However, the eccentric ones seem to get most of the press.

I am taking a short break from my higher education series of posts so that I can respond to several serious questions I received concerning the series. In this post, I will address the question of how I do mathematics and what that has to do with my thinking and writings about higher education. In several related future posts, I will deal with six famous mathematicians who have defined how the general public views mathematicians.

I was born a little too early for this scene. If computers had been around then, who knows? Image courtesy of Presenter Media.

Why was I attracted to mathematics? Was it nature or nurture? YES. Speaking like a true mathematician, I’m using the inclusive form of the conjunction “or.” Both nature and nurture led me into the world of mathematics.

I see mathematicians characterized by four traits. I believe that I was born with a rudimentary form or kernel of all four of these traits. However, I didn’t stop there. I worked very hard to cultivate the early buds of those traits in order to enhance and help them blossom into fully-formed fruit.

Simple arithmetic. Quantitative aptitude. Image courtesy of Presenter Media

I believe “Quantitative Aptitude” is the first trait a mathematician needs. This trait is a natural comfort with numbers and numerical concepts. My parents always told me that I recognized numerical differences from a very early age. I could count almost as soon as I could speak. Numbers were some of the first words that I used. I was doing simple arithmetical operations like addition and subtraction by the time I was two. I knew my multiplication tables by the time I was three. By the time I entered school, I remember “showing off” by doing three digit multiplication problems in my head without using pencil and paper. I had learned and developed a number of short-cuts and tricks to doing multiplication that I still use today.

Geometric Aptitude includes identifying geometric shapes and putting the right blocks in the right holes. Image courtesy of Presenter Media.

The second necessary trait for a mathematician is “Geometric Aptitude.” This is a natural comfort with geometric shapes and differences in sizes. I could always identify the larger piece of cake. To all who know me well, this is clearly the intersection of two of my loves: mathematics and food. From an early age, I could never get enough of either of them.

By the time I was four, I had taught myself simple division and fractions by proportioning out food. I loved the “game” of filling a square or a rectangle with smaller squares and rectangles. To make it more challenging I would include triangles. I remember one of my greatest discovery in high school was the relationship between algebra and geometry. These were two sides of the same coin. They went together like a hand in a glove.

The inverse relationship between multiplication and division came to me automatically. I was doing long division by the time I entered the first grade. The idea of a remainder was never a problem for me. I stretched my abilities by attempting more complicated long division problems “in my head” without using pencil and paper.

Mathematicians can identify patterns. Image courtesy of Presenter Media.

The third trait of a good mathematician is the ability to recognize and identify patterns. These patterns may be recurring numbers, shapes, letters, or objects. The standardized tests where an individual is shown three objects and asked to identify the next object in the sequence were always super easy for me. The patterns would just jump off the page at me. To improve my ability in identifying patterns, I kept looking for more involved sequences on which to work.

Mathematicians love to solve puzzles. We can’t get them out of our heads. Image courtesy of Presenter Media.

Jigsaw puzzles are excellent exercises to improve one’s ability to identify patterns. The patterns may be the shape of the pieces or the image that is on the piece. Deciphering cryptograms is a great exercise for finding patterns. Two more great exercises that I just recently discovered are Sudoku and Word Searches.

The fourth trait of a mathematician is a love of solving problems. Growing up I remember begging my parents to “test” me with math problems, riddles, and mysteries. We didn’t have video games back in the dark ages. Besides baseball and basketball, these were the games I loved and with which I lived. I even transformed baseball and basketball into problem-solving adventures by thinking about how to handle certain situations and then practicing those solutions on the court or diamond.

A photograph of a painting of Archimedes deep in thought by Niccolo Barabino from 1860. As a true photographic image of a 2D work of art more than 100 years old, it is in the public domain. Image courtesy of Wikimedia Commons and the Public Museum Rivoltella in Trieste.

I remember my excitement in fifth-grade when I discovered Archimedes’ method for solving problems.

Observe and analyze the situation
Propose or hypothesize solutions
Test your solutions or hypotheses
Evaluate solutions and hypotheses to find the best one
Prove your selected solution or hypothesis is right

Here was the systematic approach to problem-solving that I craved. It combined my natural intuition with logical and quantitative reasoning. I believed it fit me and I adopted it and have used it for the past 60+ years.

Within the Archimedian method are four hidden gems. Good mathematicians must be expert observers. They must have a natural intuition to be able to identify patterns and problems within the situations they encounter. Good mathematicians must be masters in the art and skill of generalization, having the ability to translate real-world problems into problems which are solvable using familiar methods or have the ability to create new methods. They must be extremely proficient in the abstract world of logic in order to “prove” their solutions are the best ones possible. The rudimentary skill and art of observation, intuitive thinking, generalization, and abstraction are innate (nature) but honed by repeated practice (nurture).

I remember four specific events that fixed my path to becoming a mathematician. Three of them occurred in fifth grade. I had a fifth-grade teacher who believed in challenging his students with tough problems to see what solutions they would propose and how they arrived at their destinations. The first defining problem for me related to the area of a triangle. Without telling us how to solve the problem, the teacher asked us to calculate the area of a triangle. I was the first in the class to propose the correct solution. I observed that any triangle could be considered as one half of a rectangle. The area of a rectangle is base times height. Therefore, the area of a triangle must be 1/2 of its base times its height.

Image of the geometric proof of the Pythagorean Theorem. This file is licensed by
its creator Blackbombchu under the Creative Commons Attribution-Share Alike 3.0 Unported license. Image courtesy of Blackbombchu and Wikimedia Commons.

The second fifth-grade event involved proving the Pythagorean Theorem. Our teacher had introduced the idea of using logic to prove certain theorems or geometric relationships. He showed us how the Egyptians constructed square corners to their buildings and pyramids using the 3-4-5 right triangle and a rope with knots tied at the three, four, and five unit marks. He suggested that in any right triangle the square of the hypotenuse was equal to the sum of the square of the other two sides. ( a²+ b²= c²).

He asked us to prove it. Again, I was the first to come up with a logically, valid proof. I used the alternating square tiles on the floor of our classroom to derive the standard geometric proof of the Pythagorean Theorem. The teacher looked at my proof and said, “Well done. You should become a mathematician.”

First 8 Rows of Pascal Triangle, created by the author of this post using ClichCahrt Software.

Later in the year, this teacher challenged us further with polynomial expansions. Starting with the straight forward multiplication of (x+y) times (x+y), he asked us to try multiplying three terms and then four terms. He asked us to do it up to ten terms.

He asked if we saw any patterns that could be generalized. As I did the repeated multiplications, I wrote the results one over the next. I saw a pattern emerging. The coefficients to combinatoric powers of x and y formed a pyramid in which an entry was the sum of the two entries above it. I had rediscovered Pascal’s Triangle.

Although I needed several hints from the teacher before I could prove the formula logically, the structure of Pascal’s Triangle suggested applications of the numbers in the triangle to not only binomial expansions but also to combinatorics (the number of possible combinations of n things taken r at a time). I went a little further and showed how this would determine the probability of the number of boys and girls in a family of a given size. This time the teacher said, “You are a mathematician.”

The fourth and final event occurred in my final year of undergraduate school. During my first three years in college, I pursued a double major in mathematics and physics. In preparing to register for my last semester, I need one more credit in physics to earn the double major. Unfortunately, the only physics courses the university was offering were courses that I had already taken or the second semester of course sequences for which I had not taken the prerequisite first semester. I asked the department chair for an independent study to complete the physics major. He hesitated for a moment and then said, “Son, I’m sorry but I’m not going to allow this. You need to stick to mathematics. You’re not a physicist. You do physics as if it were mathematics. You don’t have the intuition to be a physicist.” So I took an economics course in place of the physics course and completed undergraduate school with a B.S. in mathematics and double minors in economics and physics (one credit shy of the double major in physics.) I never looked back.

What does mathematics have to do with higher education? Higher education is built on the three foundational blocks of the creation, organization, and distribution of knowledge. The four building blocks of mathematics and the three building blocks of higher education are two sides of the same coin. The purpose of higher education is about identifying patterns and solving problems. I dealt with these two situations in every one of my positions as a faculty member or college administrator. I also found my quantitative and geometric aptitudes extremely helpful. Making things add up and fitting the right block into the correct slot were daily agenda items. Being a mathematician made me a better higher education administrator.

February 25, 2017 By B. Baylis 1 Comment

Education’s Big Lie, Part II: We Can Think without Words

As I noted at the end of Education’s Big Lie, Part I: Introduction, I have learned that we can think without words. However, in much of today’s world, particularly those parts of it touching the education enterprise, communicating without words is much more difficult, if not next to impossible. Although as the following giggleBites cartoon illustrates communicating with words can have its own drawbacks.

Image courtesy of Wikimedia Commons and Cartoosh, author of the cartoon. Wikimedia has received an e-mail confirming that the copyright holder has approved publication and is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.This correspondence has been reviewed by an OTRS member and stored in its permission archive.

One thing that the above cartoon brought forcefully to my attention is that the expression “A picture is worth a thousand words” implies “words” are the basis of value. Pictures and ideas are valued in terms of words. Have you ever heard anyone ask how much of a picture does one word equal? In any exchange of objects of value using two different currencies, one of those currencies is considered dominant. The transaction is then conducted in that currency. In education, we tend to try to force the exchange of ideas in the currency of words. We almost never let pictures speak for themselves. We have to “explain them.”

“Let me explain this idea to you.” Image courtesy of Presenter Media.

If words are our basis for the exchange of ideas, then we must have a storehouse of words to express our ideas. Aphasia is an insidious deficiency in that it steals one’s words, the basis of exchange, but not the ideas, the real objects of value. Ideas are locked inside one’s head with no easy way to communicate them.

I have managed to deal with my aphasia because of the verbal proficiency that I built up over my 60-year love affair with words. The filing cabinets in my head are filled with words. After the TBI’s, I still had a treasure trove of words in my memory which I found I could access intermittently.

Finding the right words. Image courtesy of Presenter Media

However, even with my experience and confidence with words, many times I felt words were playing “Hide and Seek” with me. Can you imagine how difficult it is for children who don’t have the same experience or comfort with words? The ideas are right there in front of the children, but they can’t find the words to express them. It’s like the “Where’s Waldo Game?” Waldo is hidden in plain sight. Let’s play “Where’s Waldo” with the dead leaf mantis in the following picture.

Can you find the bug? Somewhere in this picture is a Dead leaf mantis (Deroplatys desiccata). The picture was taken at Bugworld in the Bristol Zoo, Bristol, England. If this mantis is alarmed it lies motionless on the rainforest floor, disappearing among the real dead leaves. It eats other animals up to the size of small lizards. From the island of Madagascar, Africa. This work has been released into the public domain by its author, Arpingstone. This applies worldwide.

Having gone through my trials, I can empathize with children who must be completely bewildered when confronted with what must seem like nonsense to them. For the past eight years, it has been a constant, uphill battle for me to attempt to do the things that were second nature to me prior to the TBI’s. Even putting together these simple essays has been an exhausting task. At times, it has been an almost overwhelming chore. I have to visualize my thoughts. I must then translate those pictures into appropriate words and coherent sentences. The images that I intersperse in my posts represent the starting points of where I begin my thinking. Since I am retired, living on a fixed income, my drawing ability leaves much to be desired, I must find public domain or royalty free pictures which mirror the figures that I am seeing in my mind. I must then struggle to translate those images into words.

Where did our classrooms and education go astray? If we want to measure a child’s creativity, imagination, intelligence, curiosity, ingenuity, reasoning, and problem-solving I propose we go back and watch children play. The first picture that comes to my mind is the baby in a medical insurance television advertisement that rolls over from his back to his stomach. The baby then reaches for and grabs a soft, cloth ball. The baby then plays with the ball, feeling it, squeezing it and trying to taste it. The baby has no words to describe what he is doing. No words are spoken about what the baby is doing, but curiosity is clearly visible in the baby’s eyes and actions.

Give a one-year-old child a few crayons and the back of a paper placemat in a restaurant and watch creativity and imagination come to the fore. Give five-year-old children a new toy like a little red wagon and watch them play out interactive stories. Give six-year-old children a set of Legos and watch them build houses and monsters. Give seven-year-old children jigsaw puzzles and watch them develop problem-solving skills. In most of these situations, words are seldom to be found.

The artist was 1 year 10 months when this was drawn. Soft crayon on paper. Uploaded by the child’s parent. This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license

Since our society has dictated that our culture is passed along from generation to generation via the media of books and verbal stories, I realize that language, words, and verbal thinking must eventually come into play in education. However, I do not believe we must necessarily equate the mental characteristics of creativity, imagination, intelligence, curiosity, ingenuity, reasoning, and problem-solving with verbal thinking and verbal proficiency. I would argue that I am not alone in this position.

For more than 200 hundred years, the New York City Harbor was the first port of call for people and goods entering the United States on the east coast. It didn’t matter whether it was a military or civilian ship. It didn’t matter whether it was driven by wind or steam. It didn’t matter whether it was large or small. It headed for New York City first. For almost 1500 years, words have been the first port of call in the generation of ideas.

New York City Harbor from the Brooklyn Bridge 1893. Image courtesy of Wikimedia Commons. The image is in public domain because it was published prior to 1923.

In a number of areas outside of education, words are not the first port of call for the devotees of certain pursuits. Additionally, there have been a few brave individuals in areas dominated by words that have taken the very courageous step of coming out of the shadows and admitting that they are visual thinkers. In my next post in this series, Education’s Big Lie, Part III: Visual Thinkers in the Spotlight, I highlight a number of these individuals.

February 16, 2017 By B. Baylis 2 Comments

Education’s Big Lie, Part I: Introduction

I don’t know how to say it any clearer. I have come to the shocking conclusion that the enterprise of American education is doing society a huge disservice by propagating and perpetuating a big lie. Please do not misinterpret what I am attempting to say in this essay. I am firmly convinced that education is immensely valuable. Paraphrasing a credit card commercial campaign, it is “priceless.” For more than 65 years, my life has revolved around faith, education, and family. I am fully committed to the concept of an appropriate education for everyone. However, I am also very certain that education, as it is currently conceived and generally defined, doesn’t and can’t serve everyone equally well. To paraphrase a television commercial for a particular internet service, “Education that doesn’t serve everyone, doesn’t serve anyone.” The simplest statement of Education’s Big Lie is Procrustes’s aphorism “one size fits all.”

Caricature from 19th century German satirical magazine “Berliner Wespen” (Berlin Wasps) – Title: Procrustes. Caption: Bismarck: As I see, Lady Liberty is somewhat too large – we want to change this immediately to her contention. (He chops away her legs.) – Inscription on bed: Socialist Law. Image courtesy of Wikimedia Commons; in Public Domain

By “one size fits all” I am surprisingly not referring to either standardized testing or the Common Core. Both of these educational fads have their good and bad points. I will explicate my views on each of them in later posts. For this post, I return to a fuller statement of my understanding of the Big Lie plaguing the American educational enterprise. The reality to which I am referring is that the American educational enterprise has pigeon-holed the mental characteristics of creativity, imagination, intelligence, curiosity, ingenuity, reasoning, and problem-solving primarily if not exclusively to the verbal region of the human brain. The Big Lie equates these characteristics with one’s facility with words. Many if not most of the instruments used to measure these mental characteristics are primarily verbally based. To improve their abilities in the areas delineated above, students are instructed to read, write, and speak more.

So many books, so little time! Illustration courtesy of Presenter Media

If at first, you don’t succeed, try, try again! Draft; after draft! Illustration courtesy of Presenter Media

Why? Why did the teacher call on me? I don’t know the answer! Image courtesy of Presenter Media

This solution may work for many and possibly the majority of students. However, the problem with this remedy is that for a significant number of students words are more like enemies than friends. Words are at the crux of my argument against education. Ideas are considered the coin of the realm in education. For centuries in education, we have been indoctrinated to believe that ideas are formulated almost exclusively through words. After ideas are formed, we must then use words to express those ideas, either in written or oral form. We are taught that to think properly we must use a process that is based in and undergirded by the use of words. This process is commonly known as verbal thinking. I grew up with that mindset. In this mindset, words are the cornerstone upon which we build our ideas.

Ideas are built upon a foundation of words, phrases, and sentences. Image courtesy of Presenter Media

This was the way I was taught. It is the way most of our American society has been taught for hundreds of years. I am going out on a limb now and say that this is not the only way we think or must think. It took two traumatic brain incidents (TBI’s) in 2009 to convince me that there are other ways to think. The first TBI was the implosion of a benign meningioma due to the explosion of the artery which was feeding it. This TBI left me with a mild case of aphasia. As a verbal thinker, I found it difficult to think when I couldn’t find my beloved words.

The second TBI was a series of four tonic-clonic seizures within 30 minutes that left me in a coma for three days. When I woke up, I knew immediately something was different. I found myself no longer going directly to words to make sense of what was going on around me. I saw pictures. At first, I wasn’t certain what had happened. As I reflected on what was happening, I remember several articles that I had read that were written by stroke survivors. I was having the same experiences that they had encountered. I had become a visual thinker.

After 60 years of being a poster child for verbal thinking, words were now my second thought language, Although I was thinking in terms of pictures, I found that it was necessary for me to use words to communicate my ideas. This was extremely frustrating at times. I attempted to describe my feelings in a 2010 blog posting entitled Words Are More Like Cats Than Dogs.

Sometimes corraling words can be harder than herding cats. Image courtesy of Presenter Media

Where am I going with this argument? For centuries in educational circles, words have been king.

I am WORD! I have the final say. You must listen to me! Image courtesy of Presenter Media.

A recent Google+ posting The Importance of Imagination by Elaine Roberts, a former colleague, induced me to write this series of posts. In her posting, Roberts described a situation that led her to an epiphany and two points of clarity. The situation grew out of an attempt by a teacher to test or evaluate the creativity of a class of sixth graders. This teachers’ attempt was not a standardized test. It was a writing assignment. Most educators would label this assignment as an authentic assessment instrument. The teacher gave the children the following set of instructions:

Okay. Students, your assignment is very simple. Just write me a story about anything. Image courtesy of Presenter Media

What do I imagine some of the students heard? “Blah, Blah, Blah!”

Blah, Blah,Blah. I don’t understand what this teacher wants us to do. Image courtesy of Presenter Media

Even though they had previously been given a template to use in writing stories, what were the first thoughts of some students about constructing a story? I think they probably drew a blank.

“The teacher wants us to write a story. What am I going to do? How can I write a story? I don’t know what to write about.” Image courtesy of Presenter Media.

Taking literary license with this scenario, what did I imagine this student wanted to turn into the teacher? Simply, a blank piece of paper.

How can I write anything, if I don’t know what I should be writing about? Image courtesy of Presenter Media

What do I think the teacher’s response to a blank piece of paper woul be? Most likely, he would have said to himself, “What is wrong with this student? The wiring in his head must be all tangled up.” Now the shoe is on the other foot. The teacher doesn’t know what the student is trying to say.

“What’s up with this mixed up student? The instructions were so easy. How could not understand them? How could you turn in a blank piece of paper?” Image courtesy of Presenter Media.

With respect to the spread of the Big Lie, I readily admit that my hands are not entirely clean. Prior to 2009, as I noted above, I could have been considered a poster child for verbal thinking and verbal learning. In all of my recollections of my earliest childhood, I was constantly immersed in books and words. At the age of five, I won a Sunday School contest for being the first primary student (Grades K through 6) during the new church year to recite 100 selected verses by memory.

Yipee! I did it. I was the first to recite all 100 verses by memory.

As an academic professional, I made my living off words. Even as a mathematician, my training, and education were dominated by words. As an instructor, I constantly fed my students words.

“Okay class, who can explain Zorn’s Lemma and what is it’s relationship to the Well-Ordering Principle?” Image courtesy of Presenter Media.

As an administrator, I used words to defend positions and try to persuade colleagues to follow my lead.

Colleagues, I know the message I bring to you today at this faculty meeting will not be pleasant to hear. I want you to know that it is hard for me to have to deliver it to you. However, we are facing a huge budget deficit. I have two proposed solutions. Neither of them will be without pain. But I am bringing them to you today, to get your reactions and suggestions.” Image courtesy of Presenter Media.

With what I have written so far, I should probably call it quits for this first post in this series. If I haven’t done enough to damage my image and credibility within the higher education community, I invite you to stay tuned for additional posts. Although it has been difficult at times, I have learned that we can think without words. In fact, I have subtitled Part II of the series Education’s Big Lie, “We Can Think without Words.” Even though we give lip service to the idea that “A picture is worth a thousand words”, in much of today’s world, particularly those parts of it touching the education enterprise, the most difficult aspect of working with thoughts and ideas is trying to communicate them without words.